Vidutinė reikšmė (kartais dar vadinama tiesiog vidurkiu) gali būti aprašoma keliais būdais. Toliau kalbėsime, kaip apskaičiuoti vidutinę reikšmę, priklausomai nuo to, kokius pradinius duomenis turime ir kokių galutinių rezultatų tikimės.

Vidurkis yra naudojamas norint apibūdinti turimus skaičius ir pateikti vieną reikšmę dideliam duomenų kiekiui apibendrinti. Žemiau pateikiami keli vidurkio naudojimo pavyzdžiai:

• kelionės trukmė iš namų į darbą kiekvieną dieną truputį skiriasi. Vidutinė laiko trukmė gali būti naudojama, norint geriau suprasti, kiek apytiksliai laiko užtruks ši kelionė;
• skaičiuojant lauko, reikalingo kokiam nors darbui vidurkį, galima planuoti dienos grafikus, siekiant užtikrinti, kad būtų pakankamai laiko visai veiklai;
• jei studentas skaito tam tikrą vadovėlį su n skyrių per x valandų, galima apskaičiuoti vidutinį kitų panašių vadovėlių ir skyrių skaitymo laiką. Tai padės studentui geriau planuoti laiką, norint pasiruošti egzaminui;
• norėdama apibendrinti ir įvertinti savo veiklą, įmonė gali skaičiuoti tam tikro laikotarpio vidutinį klientų, pardavimų ar darbuotojų skaičių;
• finansų specialistai gali apskaičiuoti vidutinę įmonės akcijos kainą, kadangi įmonės akcijų kaina kinta kiekvieną dieną;

Aritmetinis vidurkis 

Aritmetinis vidurkis yra labiausiai paplitęs ir įprastas vidurkio tipas. Tam tikrų skaičių aritmetinis vidurkis yra skaičius m, kuris lygus turimų skaičių sumai padalintai iš visų skaičių kiekio. Labai dažnai kalbant apie aritmetinį vidurkį, jis vadinamas tiesiog „vidurkiu“.

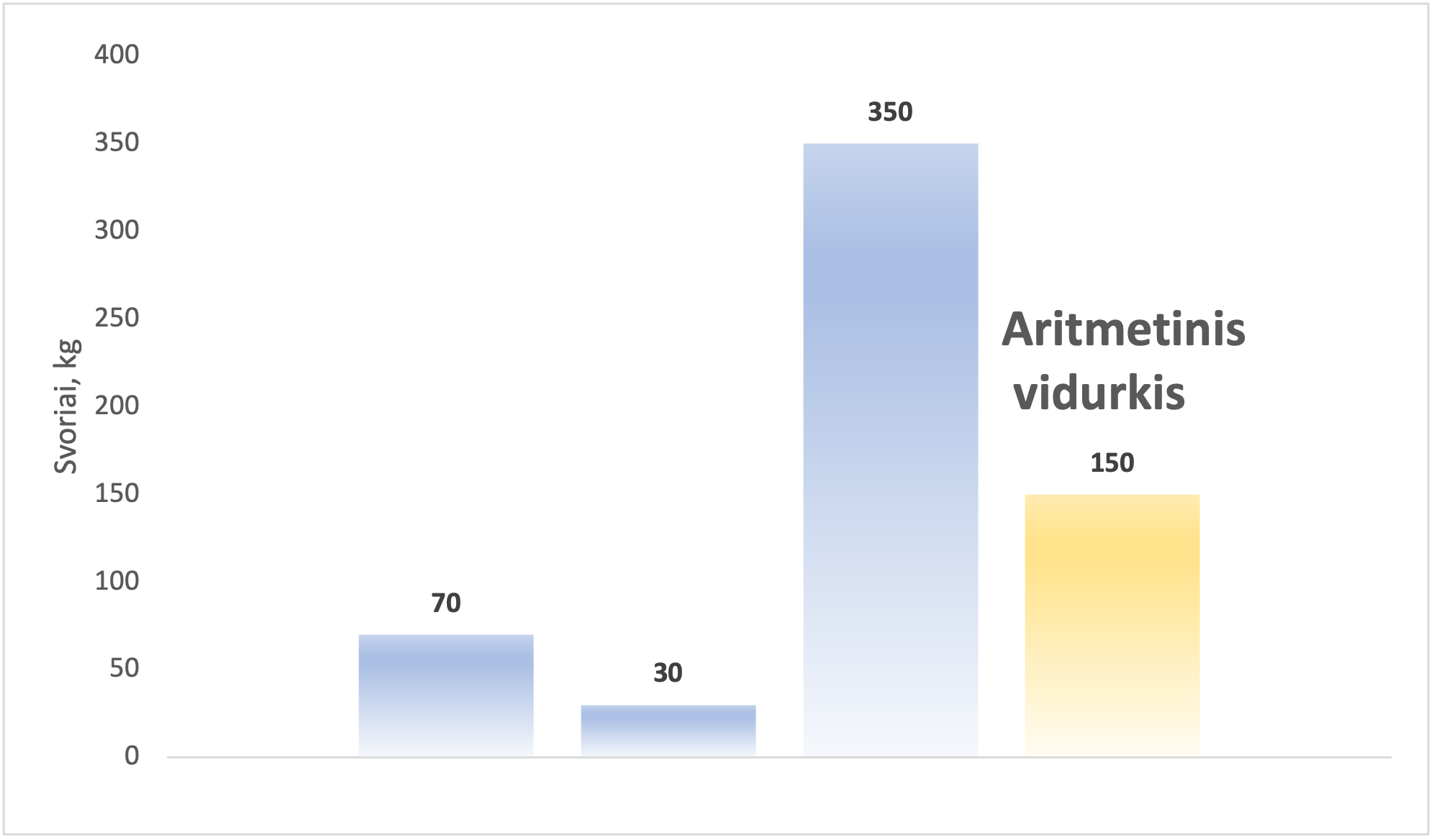
Tarkime, kad sveriate 70 kg ir lifte esate kartu su 30 kg sveriančiu vaiku bei 350 kg sveriančiu vėpliu. Koks būtų visų važiuojančių svorių aritmetinis vidurkis? 

Kitaip tariant: jei šią linksmą kompaniją pakeistumėte 3 vienodais žmonėmis ir norėtumėte, kad lifte būtų tokia pati apkrova, kiek turėtų sverti kiekvienas žmogus? Šiuo atveju kiekvienas žmogus turi sverti po 150 kg (skaičiavimas: (70 + 30 + 350)/3 = 150), kad lifto apkrova išliktų ta pati. Norint apskaičiuoti vidurkį, reikia bent dviejų skaičių. Norint gauti prasmingą rezultatą, šie skaičiai turėtų matuoti ar apibūdinti tą pačią objekto ar reiškinio savybę, pavyzdžiui, temperatūros rodmenys, kavos kaina,  širdies dūžių skaičius per minutę, mokinių egzaminų įvertinimai ir t. t. Negalima skaičiuoti vidurkio, sudedant skirtingas savybes, pvz. svorį ir ūgį. 

Aritmetinio vidurkio privalumai: 

• Gerai naudoti skaičiams, kurie gali būti sudedami kartu. 
• Lengva apskaičiuoti: reikia tik sudėti ir padalinti. 
• Jį lengvai suvokiame intuityviai – tai skaičius, apibūdinantis vidutinę kokios nors savybės reikšmę. Jį padidina didelės reikšmės ir sumažina mažos. 

Aritmetinio vidurkio trūkumai: 

• Vidurkis gali būti iškreiptas dėl labai išsiskiriančių reikšmių – jo nereikėtų taikyti, kai skaičiai turi labai skirtingas reikšmes. 100, 200 ir -300 aritmetinis vidurkis yra lygus 0, o tai klaidina, nes blogai apibūdina turimus skaičius. 

Aritmetinis vidurkis puikiai tinka 80% atvejų. Deja, visada yra tie 20 procentų situacijų, kai šis dydis ne visai tinka.